El Universo tiene problemas de los tres cuerpos reales: qué son y dónde están
El problema de los tres cuerpos, un reto matemático que surgió junto con las leyes de la mecánica y gravitación de Isaac Newton, se refiere a la imposibilidad analítica de conocer la estabilidad y predecir las trayectorias de tres o más objetos interactuando gravitacionalmente entre sí. Recientemente, se ha popularizado por la aclamada serie de Netflix y el libro del mismo nombre. En el universo existen gran cantidad de ejemplos, siendo la regla y no la excepción de los sistemas estelares conocidos.
Sobre el movimiento de los astros
En el deseo de la humanidad de interpretar su entorno ha desarrollado herramientas matemáticas para predecir el comportamiento de, entre otros muchos ejemplos, los astros. Numerosos intentos surgieron a lo largo de las décadas, algunos con mayor precisión que otros, pero sin una respuesta definitiva. Al menos no hasta las formulaciones de Isaac Newton.
Newton no encontró únicamente una expresión simple para derivar el movimiento de los astros, sino que desarrolló las herramientas matemáticas para poder explotar todo su potencial. Empleando el cálculo logró demostrar las famosas tres leyes del movimiento planetario de Johannes Kepler.
Por medio de ciertas simplificaciones se puede reducir el problema del movimiento de la Tierra a un sistema de dos cuerpos, comprendido por el planeta y el Sol, donde la masa de la primera es mucho menor que la del segundo. Esto genera la posibilidad de predecir de una forma exacta la posición y velocidad en cualquier momento.
Perturbaciones gravitacionales
Es normal pensar que resolver un problema con un único cuerpo adicional no tendría mayor complejidad. No obstante, al querer estudiar tres o más objetos de forma general aparece un gran inconveniente. Las técnicas de solución, por medio de encontrar constantes de movimiento como el momento lineal del sistema o la energía total, resultan infructíferas. Sin importar el camino que se tome, es imposible encontrar una solución absoluta y general a la posición y velocidad de cada objeto en un momento cualquiera dado.
Cabe resaltar un aspecto importante, la incapacidad de encontrar una solución exacta y directa no implica estrictamente que no existan métodos o simplificaciones para estudiar la evolución de un sistema.
Un caso particular es el llamado problema de los tres cuerpos restringido, donde se suponen limitaciones que simplifican en gran medida la dificultad. En este escenario se tiene que uno de los tres cuenta con una masa significativamente menor a las otras dos, como un sistema comprendido por un planeta y dos estrellas. De tal manera que los dos cuerpos mayores ignoran la presencia del tercero. Bajo otras restricciones se encuentra un sistema con cinco puntos de estabilidad, conocidos como punto de Euler-Lagrange o simplemente de Lagrange. Corresponden a lugares matemáticos donde la atracción gravitacional y la fuerza centrífuga se contrarrestan. Esto es aprovechado por misiones como James Webb o DSCOVR.
Por otro lado, cuando se desea estudiar la dinámica de los objetos, no siempre es posible contar con dichas suposiciones. En este caso se emplean herramientas numéricas que por medio de evolucionar el sistema al cabo de pequeños saltos de tiempo es capaz de ofrecer una aproximación al comportamiento real.
Sistemas estelares múltiples reales
Gracias a estudios se ha podido realizar un análisis de los tipos y correspondientes distribuciones de los sistemas estelares de la Vía Láctea. Entre ellas se encuentra una mayor proporción de enanas rojas y un considerable número con dos o más estrellas.
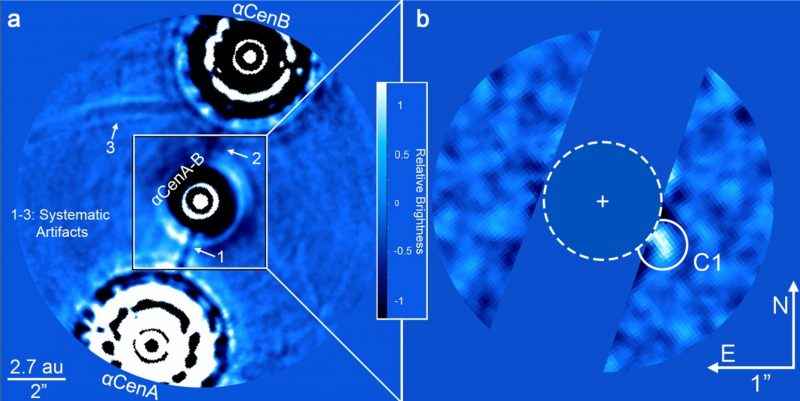
El primer y más cercano ejemplo de un sistema estelar de tres objetos es Alfa Centauri a 4,26 años luz de la Tierra. Como su nombre indica, es el objeto más brillante de la constelación del centauro y se comprende por las estrellas Alfa Centauri A, B y C, esta última también conocida como Próxima Centauri. Además, cuenta con un planeta oficialmente reconocido y otro candidato a exoplaneta.
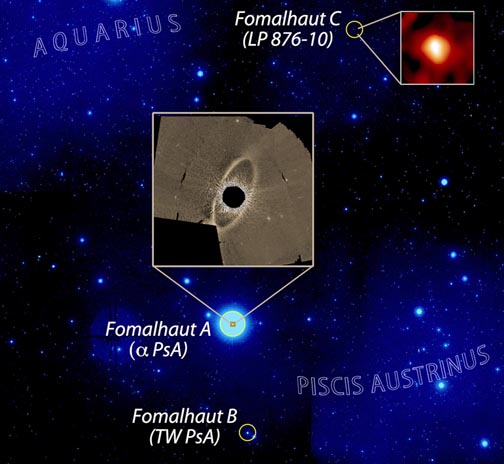
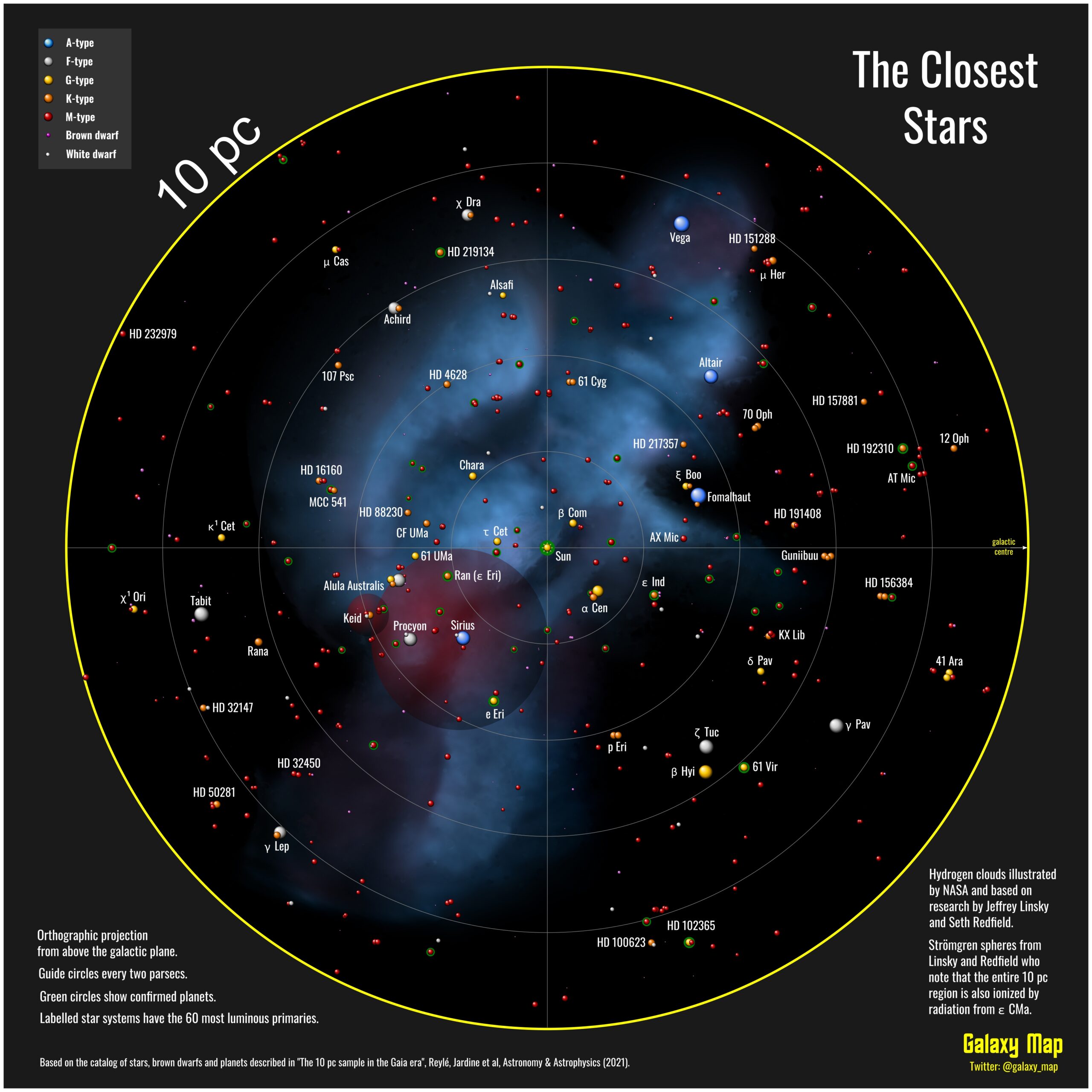
Al estudiar los objetos a menos de 10 parsecs, o aproximadamente 32 años luz de la Tierra, aparecen varios otros ejemplos de sistemas de dos, tres o hasta cuatro estrellas atadas gravitacionalmente. De los objetos más famosos del cielo se tiene a Sirio o Spica, cada una con una acompañante, Polaris, Fomalhaut y Alfa Centauri, comprendidos por tres elementos, Capella y Mizar son sistemas cuádruples. Mintaka, parte del cinturón de Orión, es un sistema quíntuple.
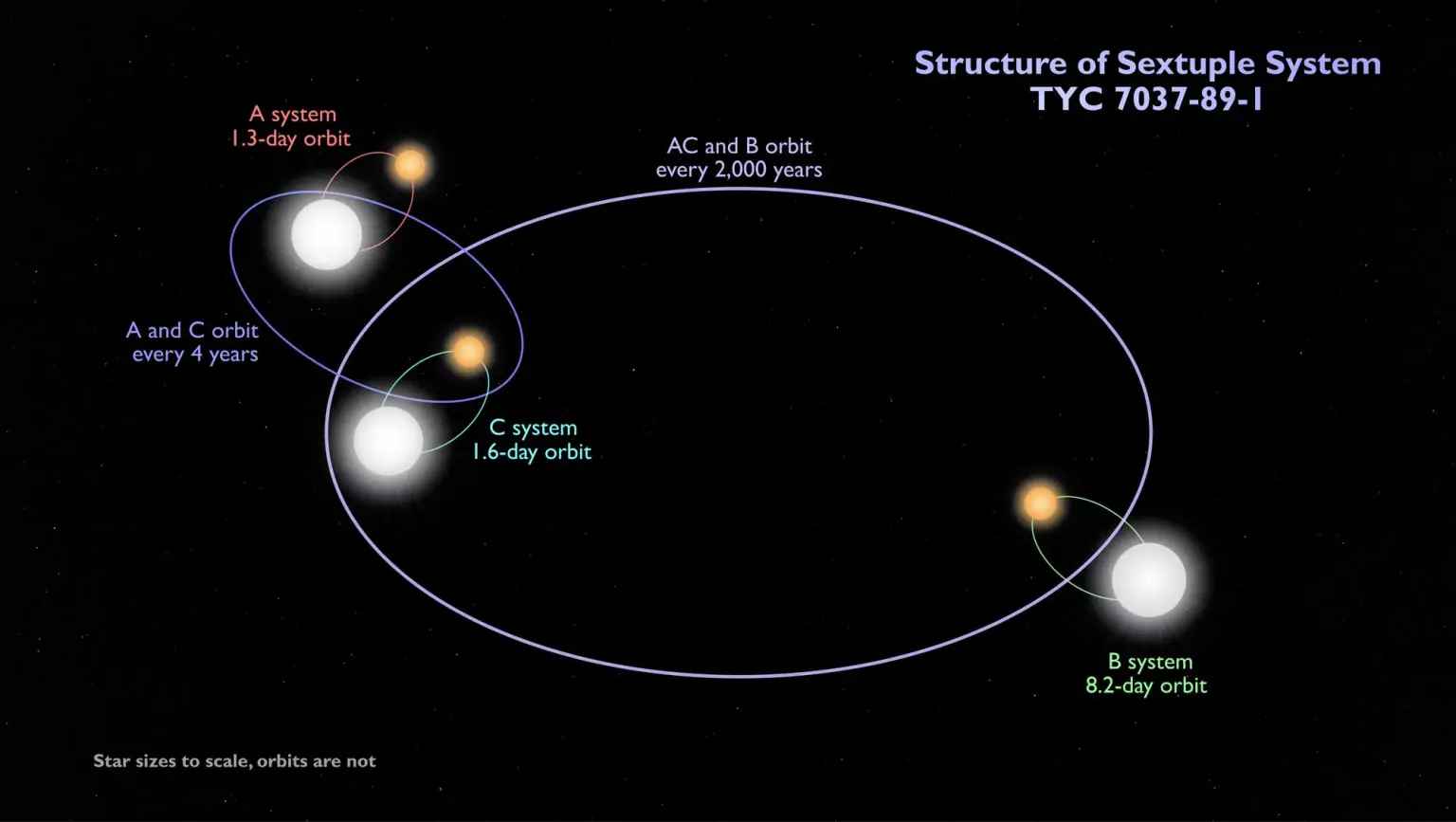
Ejemplares extremos y considerablemente extraños pueden contar incluso con seis elementos, aunque el número puede seguir creciendo. TYC 7037-89-1 es un sistema estelar séxtuple, tres pares de estrellas se orbitan mutuamente y dos de estas danzan entre sí. Donde el otro par se mueve alrededor de las dos primeras. QZ Carinae es un sistema múltiple complejo con un total de nueve estrellas conocidas a 7500 años luz de la Tierra.
El orden en un sistema caótico
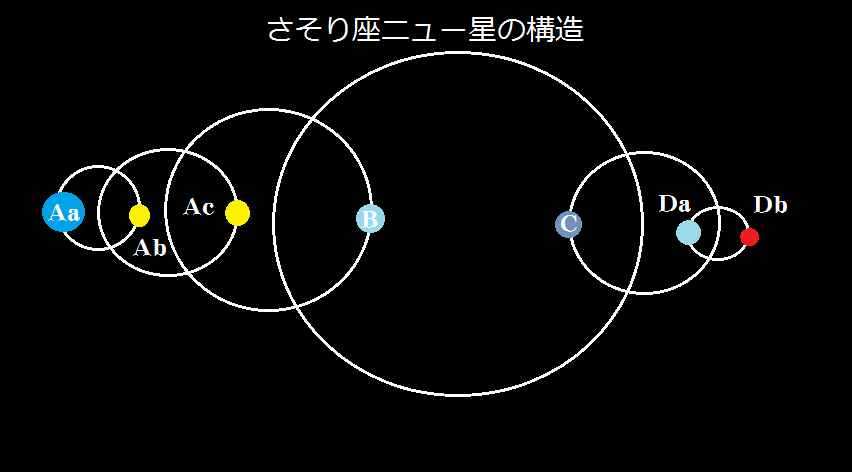
Cuando se habla del problema de los tres cuerpos se menciona que este es un sistema caótico. Este concepto es erróneamente entendido como que es intrínsecamente inestable. Si bien puede ser el caso para una tripleta de estrellas, este concepto se refiere realmente a que bajo pequeños cambios en las condiciones iniciales, al cabo de un cierto tiempo los escenarios divergen considerablemente.
Por ejemplo, desplazar unos pocos centímetros a Mercurio, bien sea hacia o en contra del Sol, implica un futuro donde varios planetas pueden caer a la estrella o ser eyectados del sistema.
Sin embargo, ser un sistema caótico no implica que no exista un orden. Hay numerosos procesos que pueden, por ejemplo, formar pares o tripletas de estrellas, que posteriormente pueden acoplarse gravitacionalmente con otros. La propia interacción entre los distintos componentes se encarga de buscar un estado de mínima energía, que en la mayoría de los casos corresponde a una configuración que permite la estabilidad en el tiempo.
Esta entrada fue modificada por última vez en 05/04/2024 21:33