Una de las incógnitas que perseguía a los grandes pensadores de la humanidad era el cómo se movían los planetas y deseaban poder encontrar una forma efectiva de predecir su comportamiento. Sin embargo, a partir de datos brutos de miles de observaciones se consiguieron obtener las famosas leyes de Kepler, una forma fácil de entender el comportamiento de los planetas al rededor del sol y aquí te lo cuento.
Te interesa: Así es como los cohetes alcanzan el espacio
Creando un mapa de las estrellas
Tycho Brahe fue un personaje muy importante para la historia, aprovechando el 4% del producto interno bruto de Dinamarca; otorgado por el rey de aquella época, construyó un complejo cuyo objetivo era de realizar las efemérides más completas posibles.
Empleando decenas de diversos instrumentos, y en una época en la cual todavía el telescopio no era usado para observar el cielo, posibles. Empleando decenas de diversos instrumentos, se le considera como el más grande observador del cielo antes del uso del telescopio en ámbitos astronómicos. Él y su equipo crearon un registro continuo de la posición de las estrellas, planetas y demás objetos en la bóveda celeste.
Poco después de su muerte, Johannes Kepler consiguió acceso a todos esos datos. En la época aún existía el misterio del porqué Marte pasaba por un fenómeno conocido como movimiento retrógrado; en el cual el planeta parece detenerse, retroceder y volver a avanzar, que no era explicado satisfactoriamente por ningún modelo del sistema solar. Es así como él, a partir de los registros de Brahe, propone un modelo y tres leyes que regían el movimiento de los astros.
Las tres leyes del Kepler sobre el movimiento planetario
Los planetas tienen trayectorias elípticas con el sol en uno de sus focos
Para empezar ya se obtiene bastante información de sobre la forma de la trayectoria que trazan los astros alrededor del Sol, a través de círculos achatados o elipses. En este caso aparecen 2 términos nuevos, perihelio y afelio, es decir, el punto más cercano y lejano de la órbita, respectivamente.
Una vez se conoce la forma general de la trayectoria, se pueden emplear diferentes herramientas matemáticas para poder entender mejor los fenómenos observados. Y, de hecho, es a partir de esta geometría especial de las elipses que se construyen las siguientes leyes.
Un planeta recorre áreas iguales en tiempos iguales
Junto con las observaciones realizadas por Tycho Brahe y los análisis de Johannes Kepler de estas, se observaron diferentes cambios en las velocidades lineales de los planetas dependiendo de su distancia respecto al sol. Pero a su vez aquellos cambios suponían una cantidad conservada; algo muy importante en física, y resulta de gran utilidad para poder entender de mejor manera la gravedad.
Sin importar en que dirección al Sol se observara un planeta, con dejarlo moverse durante un tiempo fijo debería de siempre cubrir la misma área entre descrita por su trayectoria y el foco de la elipse, esto gracias al cambio en la velocidad según la distancia a la estrella.
El cuadrado del periodo es directamente proporcional al cubo del semieje mayor
Para poder caracterizar una elipse se requieren de 2 números fundamentales, la excentricidad; un número que toma valores mayores iguales a cero y menores a uno que describen cuan achatada es, y el semieje mayor; la longitud comprendida entre el centro y el punto más lejano. Luego, para entender las órbitas se utiliza el periodo, el cual se refiere al tiempo que le toma a un planeta completar una revolución alrededor del Sol.
En conjunto, estos dos valores mantienen una relación intrínseca y muy útil al estudiar el movimiento de los planetas, de forma tal que conociendo uno puedes conocer sin mayor problema al otro. Sin embargo, aquella constante que servía como transformación entre el periodo y el semieje mayor no se conocía la forma de calcularla y fue necesario estimarla a partir de observaciones directas de los entonces conocidos seis planetas.
Newton y la ley de gravitación universal
Inspirado por los trabajos de Johannes Kepler sobre el estudio del movimiento de los planetas alrededor del Sol, Newton quería desvelar no solo la dinámica que los rige; es decir, estudiar exclusivamente el movimiento, sino ir un paso más allá y desentrañar la mecánica que lo hacía posible; es decir, las fuerzas que se encargan de inducir aquellas peculiares trayectorias.
A partir del análisis de la Luna y los planetas, encontró que una fuerza atractiva cuya magnitud era directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que separa ambos objetos funcionaba increíblemente bien para predecir y justificar las órbitas planetarias y, pero con menor precisión, la de la Luna alrededor de la Tierra.
Es así como nace la ley de gravitación universal de Newton, una forma sencilla pero increíblemente poderosa para explicar no solo el movimiento de los astros, sino también era aplicable a nuestra vida cotidiana. Por ejemplo, con la gravedad se puede entender correctamente el periodo de oscilación de un péndulo, el tiempo de caída de algún objeto con una distancia dada, la distancia aproximada que recorrería una bala de cañón, entre otras muchas cosas.
El problema de los dos cuerpos
En física y matemáticas se entiende a “solucionar las ecuaciones de movimiento” como poder conocer toda la dinámica; movimiento, de un sistema bajo ciertas fuerzas. En este caso; Sol y planeta, se le llama el problema de dos cuerpos y dado que nuestra estrella tiene una masa varios órdenes de magnitud más que los cuerpos que la orbitan, se convierte en un problema de un cuerpo. Con esta simplificación y a través de herramientas matemáticas se obtienen sin mayor problema las leyes de Kepler.
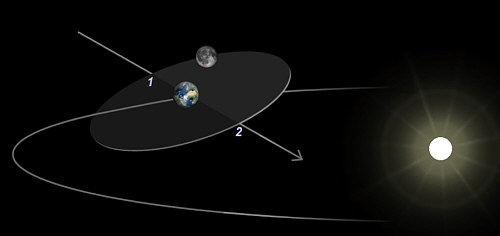
Kepler no solamente hizo un trabajo fascinante al derivar sus leyes única y exclusivamente a partir de observaciones, sino que sus hallazgos resultaron ser correctos para el sistema que se estudiaba. Aquellas leyes de Kepler sobre el movimiento de los planetas también se puede extender a las lunas y a los satélites que no se encuentran muy lejos de la Tierra.
Esta entrada fue modificada por última vez en 02/04/2024 20:45