Marcus Chown: “Por qué el universo real tiene un gemelo matemático que lo imita en todos los sentidos sigue siendo un misterio”
20/04/2021 Redaccion
Enrique Sacristán/SINC
Las predicciones matemáticas de fenómenos y objetos totalmente desconocidos a veces se hacen realidad y se observan por primera vez en el universo: nuevos planetas, agujeros negros, antimateria, neutrinos, ondas gravitacionales… El escritor y divulgador británico Marcus Chown relata en su última obra esos momentos ‘mágicos’ que cambiaron la historia de la ciencia y cómo los vivieron sus protagonistas.

Una despejada noche de 1846, cuando se apagaron las farolas en Berlín, el astrónomo alemán Johann Galle y su ayudante apuntaron el telescopio hacia el lugar del cielo donde un matemático francés, Urbain Le Verrier, les había dicho que encontrarían un nuevo planeta. Y efectivamente los cálculos no fallaron, allí estaba: acababan de descubrir Neptuno.
Este es uno de los diez asombrosos descubrimientos que cuenta el divulgador científico Marcus Chown (Londres, 1959) en el libro El instante mágico (Blackie books), un viaje a momentos clave de la física donde algunos investigadores descubren lo que otros antes ya habían predicho, como las ondas electromagnéticas (formuladas por J. C. Maxwell, demostradas experimentalmente por Heinrich Hertz), la antimateria (Paul Dirac, Carl D. Anderson), los neutrinos (Wolfgang Pauli, Clyde Cowan y Frederick Reines), el bosón de Higgs (Peter Higgs, CERN) o la reciente detección por parte del observatorio LIGO de las ondas gravitacionales que vaticinó Einstein hace un siglo.
¿Cómo has elegido a los protagonistas de tus historias?
El libro trata de lo que llamo la “magia central de la ciencia”: el hecho de que sea posible escribir una fórmula matemática que predice la existencia de algo insospechado, y que cuando la gente lo va a buscar, encuentra que existe realmente en el mundo real. Así que las personas que seleccioné fueron las que demostraron esta magia con más fuerza, prediciendo la existencia de Neptuno, la antimateria, los agujeros negros, etc.
Hablas de los científicos como ‘magos’, pero se supone que la ciencia y la magia son cosas muy diferentes…
Utilizo la palabra “mago” de una manera colorida y poética. Por supuesto, no creo que los científicos sean realmente magos. Sin embargo, lo que hacen, predecir cosas previamente insospechadas con sus ecuaciones, es tan extraordinario que muchos investigadores apenas pueden creerlo. El propio Einstein no se creía dos predicciones de su teoría de la relatividad: los agujeros negros y el universo en expansión.
Todavía no entendemos lo que el físico y matemático Eugene Wigner llamó “la irracional eficacia de las matemáticas en las ciencias naturales”. Por qué el universo real tiene un gemelo matemático que lo imita en todos los sentidos sigue siendo un misterio, una pieza de ‘magia’ inexplicable.
Los agujeros negros fueron predichos por un hombre que se estaba muriendo en un hospital de campaña durante la I Guerra Mundial, y luego fueron codescubiertos por otro que lo celebró invitando a helados a sus hijos junto a la playa. ¿Puede haber mayor contraste?
¿Cuáles son tus historias favoritas de El instante mágico, sin entrar en los detalles que se pueden leer en tu obra?
Son esos detalles originales los que espero den vida al libro. Por ejemplo, me gusta el hecho de que el físico que predijo el neutrino [W. Pauli] apostara una caja de champán a que nadie sería capaz de detectarlo. Además lo predijo en el peor año de su vida: su madre se había suicidado, su mujer se había ido con otro científico que vivía cerca, y él estaba tan desesperado que tuvo que pedir ayuda al psicoterapeuta Carl Jung.
Luego está el caso de los agujeros negros. Fueron predichos por un hombre [Karl Schwarzschild] que se estaba muriendo de una dolorosa enfermedad de la piel en un hospital de campaña durante la Primera Guerra Mundial, y sin embargo estos objetos fueron codescubiertos por otro personaje [Paul Murdin] que lo celebró invitando a sus dos hijos pequeños a un helado en una cafetería junto al paseo marítimo de una ciudad costera inglesa. ¿Puede haber mayor contraste?
La otra codescubridora fue Louise Webster, una de las pocas mujeres que aparecen en tu libro. Supongo que no aparecen porque esa era la realidad…
Desgraciadamente tienes razón. Ha sido difícil para las mujeres en el pasado. Me complació especialmente destacar a Louise Webster, que murió trágicamente joven. Nadie ha oído hablar de ella ni de que fue la codescubridora de los agujeros negros [junto a Murdin confirmó que una estrella giraba alrededor de uno de estos oscuros objetos]. En 2020 el Premio Nobel fue para los agujeros negros, pero nadie la mencionó, ni tampoco a su compañero.
Cecilia Payne descubrió de qué está hecha la mayor parte de la materia del universo, pero su supervisor le hizo decir que el resultado seguramente sería erróneo. Una década después, cuando se hizo evidente que ella tenía razón, él se llevó el mérito
Aunque no aparezcan en tu libro, no es el único caso de físicas ninguneadas, ¿verdad?
De hecho, solo cuatro han ganado el Premio Nobel. Otro ejemplo: entre los tres premiados con el Nobel por los púlsares ninguno fue a parar a su descubridora: Jocelyn Bell. Y pocos han oído hablar de Cecilia Payne, que escribió el doctorado en astronomía más importante del siglo XX. En la década de 1920, utilizó la recién estrenada teoría cuántica para decodificar la luz del Sol, descubriendo que el 98 % de sus átomos eran hidrógeno y helio. Descubrió de qué está hecha la mayor parte de la materia del universo, pero su supervisor, Henry Norris Russell, le hizo decir en su tesis que el resultado seguramente sería erróneo. Una década después, cuando se hizo evidente que ella tenía razón, él se llevó el mérito.
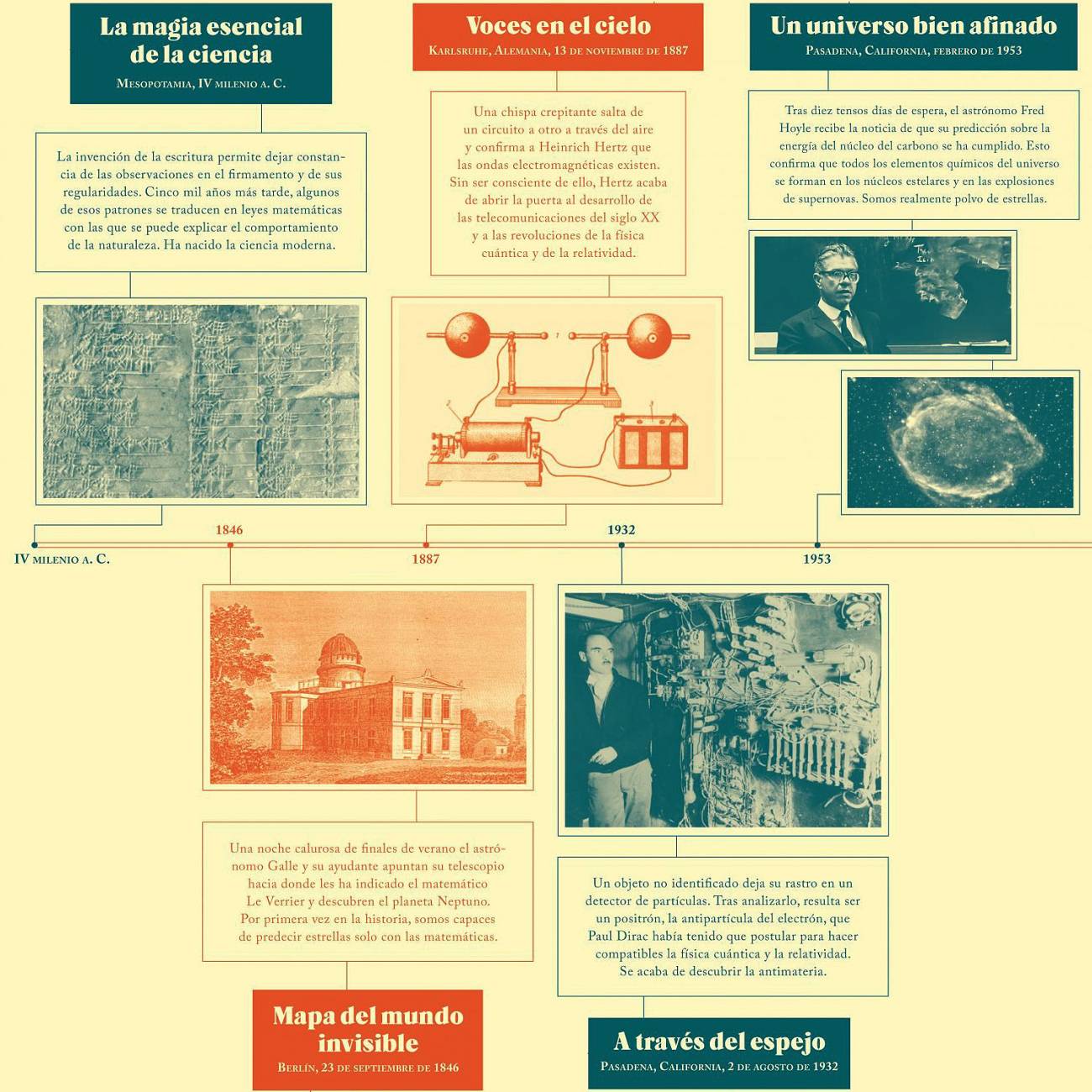
Algunos ‘instantes mágicos’ hasta mediados del siglo XX. / Blackie books
Volviendo a esa ‘magia’ de las matemáticas para describir la realidad física ¿Qué piensas sobre esa capacidad que tienen para revelar o predecir los secretos del universo?
Me sigue sorprendiendo. Como dijo Paul Dirac, “¿por qué la naturaleza está construida de esta manera? Uno solo puede responder que nuestros conocimientos actuales parecen mostrar que la naturaleza está construida así. Simplemente tenemos que aceptarlo. Quizá se podría describir la situación diciendo que Dios es un matemático de muy alto nivel y que utilizó matemáticas muy avanzadas para construir el universo”.
Pero cuando Dirac dice que “Dios usó bellas matemáticas para crear el mundo” no se refiere a un dios real, sino a una metáfora de la naturaleza, ¿no?
Sí, para Dirac y Einstein (aunque no para Newton) dios era simplemente una metáfora. Ambos podrían haber dicho que el universo está construido según líneas matemáticas en lugar de evocar a Dios. Una de las cosas más sorprendentes del universo físico es que se pueden explicar muchas cosas sin invocar a un ser supremo.
¡Espero que el universo sea matemático, que estemos realmente en el camino correcto!, pero no lo sé
¿Consideras que todo el universo es matemático o sólo lo parece, como dice tu compatriota, el científico Stephene Wolfram?
El punto de vista de Wolfram es muy convincente. Sin embargo, si es cierto, significaría que solo estamos viendo una pequeña fracción de los fenómenos del universo, aquellos que pueden ser captados por las matemáticas; y que va a ser difícil observar el resto, ya que sería resultado de la computación [que se podría describir con sencillos programas informáticos capaces de generar una enorme complejidad]. ¡Pero yo espero que el universo sea matemático, que estemos realmente en el camino correcto!, pero no lo sé.
En el pasado, los grandes descubrimientos surgían de mentes individuales, como Galle y Le Verrier, pero ahora parecen lograrlos grandes grupos de científicos, como los del CERN o LIGO. ¿Hay alguna diferencia entre los físicos y los matemáticos en este sentido?
Interesante pregunta. De hecho, hay dos tipos de predicciones en física: las realizadas por individuos como Newton y Einstein, y las que proponen grupos de cinco a diez personas, normalmente a lo largo de una década más o menos, como la teoría cuántica y el modelo estándar. Estoy bastante seguro de que esto ocurre también ahora con las matemáticas. Hay individuos que hacen descubrimientos, pero también hay grupos de personas que investigan juntas.
Durante un periodo de peste, Newton, aislado en la granja de su familia, descubrió la ley universal de la gravedad. Quizá en estos tiempos de covid surja un nuevo Newton que revolucione también la ciencia
Probablemente, el trabajo en equipo es cada vez más importante tanto en matemáticas como en física, ¡aunque todos esperamos un nuevo Newton, Einstein o Gauss! Curiosamente, fue en el periodo de la peste de 1665-1666 cuando Newton, aislado en la granja de su familia, descubrió la ley universal de la gravedad y transformó la ciencia. ¡Quizás en este año de covid surja un nuevo Newton que revolucione la ciencia!
¿Alguna predicción de las matemáticas que pudiéramos observar en el universo en los próximos años?
En cuanto a la física fundamental, la última predicción del modelo estándar, el bosón de Higgs, se encontró en 2012. Ahora realmente estamos atascados porque no podemos fusionar la teoría cuántica (la descripción de lo muy pequeño) con la teoría de la gravedad de Einstein (la descripción de lo muy grande). Si pudiéramos, habría muchas predicciones.
Sin embargo, una aproximación a la gravedad cuántica es la gravedad cuántica de bucles, que pronostica que el universo se contrajo hasta un Big Crunch (gran implosión o colapso) antes de explotar en el Big Bang. Eso habría dejado una huella en la radiación cósmica de fondo, el afterglow (resplandor crepuscular) del Big Bang, y en la próxima década podríamos ver esa huella desde el espacio.

‘Instantes mágicos’ de las últimas décadas. / Blackie books
Comparte esto:
- Entrada
- Haz clic para compartir en Threads (Se abre en una ventana nueva) Threads
- Haz clic para compartir en WhatsApp (Se abre en una ventana nueva) WhatsApp
- Haz clic para compartir en Reddit (Se abre en una ventana nueva) Reddit
- Haz clic para compartir en Telegram (Se abre en una ventana nueva) Telegram
- Haz clic para compartir en Mastodon (Se abre en una ventana nueva) Mastodon
- Haz clic para compartir en Bluesky (Se abre en una ventana nueva) Bluesky