Entrelazamiento: el mayor misterio de la física cuántica
El entrelazamiento es posiblemente el fenómeno más intrigante de la física cuántica, el que más se aparta de nuestras expectativas basadas en el sentido común. Para entenderlo, y considerar su importancia, hemos de hacer un poco de historia.
El entrelazamiento cuántico fue descubierto sobre el papel por Einstein, Podolsky y Rosen en 1935; y parece tan absurdo que ambos afirmaron que era una prueba de que la física cuántica debía ser incorrecta, o al menos incompleta. Sin embargo, el absurdo fenómeno es real, como demostraron en el laboratorio los galardonados con el premio Nobel de física de 2022, John Clauser, Alain Aspect y Anton Zeilinger.
¿Qué es el entrelazamiento cuántico?
Pensemos en una partícula cualquiera, por ejemplo, un electrón. Un electrón posee varias propiedades físicas: su masa, su carga eléctrica y su espín.
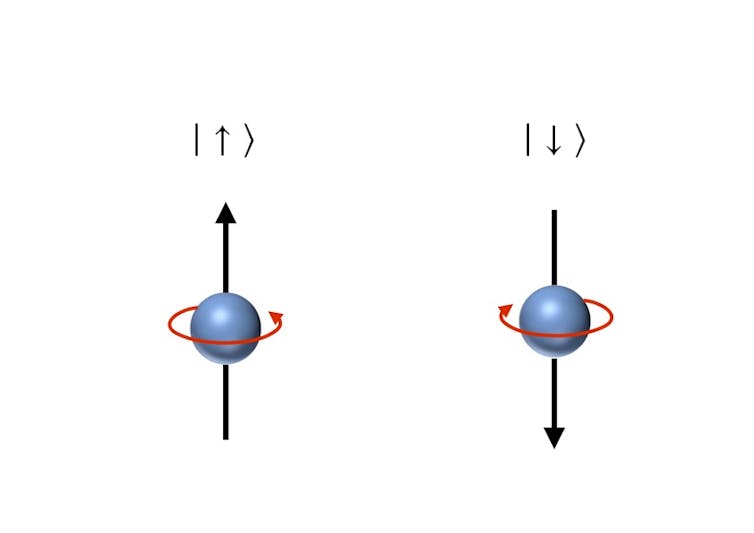
El espín de una partícula es su giro intrínseco. Podemos imaginarlo como si la partícula fuera un planeta en miniatura que rota alrededor de un eje. Habitualmente se representa mediante una flecha que apunta en la dirección de avance de un tornillo girando de la misma forma que la partícula. En el caso de la Tierra, sería una flecha a lo largo del eje de rotación de la Tierra y apuntando hacia arriba (hacia la estrella polar). Usando la notación de la física cuántica, los dos estados básicos del espín son | ↑ ⟩ (espín apuntando hacia arriba) y | ↓ ⟩ (apuntando hacia abajo):
Supongamos ahora que tenemos dos partículas (electrón 1 y electrón 2), ambas con el espín apuntando hacia arriba. Su estado es | ↑ ⟩₁ | ↑ ⟩₂ :
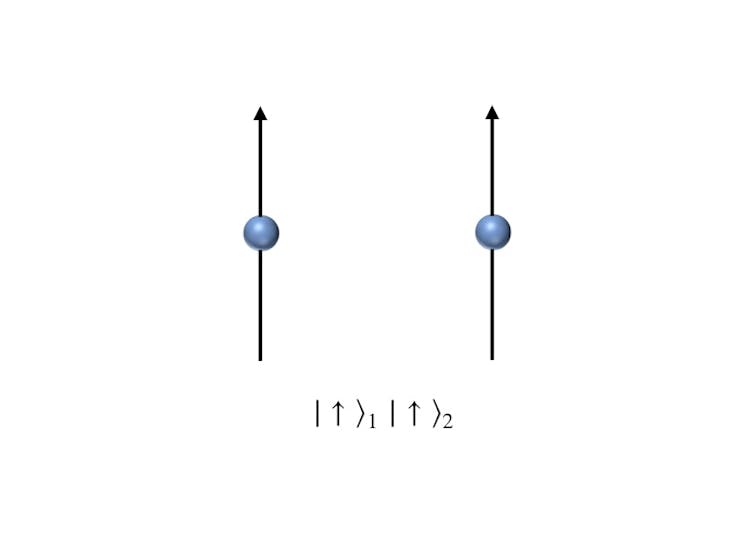
Análogamente podríamos considerar un estado con los dos espines apuntando hacia abajo, | ↓ ⟩₁ | ↓ ⟩₂ .
Ahora bien, según la física cuántica el sistema de los dos electrones podría estar en una superposición de ambos estados:
| ↑ ⟩₁ | ↑ ⟩₂ + | ↓ ⟩₁ | ↓ ⟩₂
En esta situación las dos posibilidades conviven: los dos espines apuntando hacia arriba y los dos hacia abajo. Es lo que se llama un estado entrelazado, en el cual no es posible atribuir un estado de espín definido a ninguno de los electrones. Si medimos el espín de la partícula 1, podremos obtener ↑ o ↓ con una probabilidad del 50 %. Y lo mismo si optamos por medir el espín del electrón 2.
Ahora viene el punto clave. Supongamos que medimos el espín del electrón 1 y obtenemos ↑. Entonces el estado deja de ser una superposición, ya que la posibilidad ↓ queda automáticamente excluida. Por tanto, solo uno de los términos de la superposición anterior sobrevive, concretamente el primer término, | ↑ ⟩₁| ↑ ⟩₂ :
| ↑ ⟩₁| ↑ ⟩₂ + | ↓ ⟩₁| ↓ ⟩₂ ⎯→ | ↑ ⟩₁| ↑ ⟩₂
Este cambio del estado, solo por ser observado, se denomina colapso del estado, y es un postulado de la mecánica cuántica en su formulación más ortodoxa.
El punto importante es que ahora el espín del segundo electrón ya no puede ser ↑ o ↓ con una probabilidad del 50 %. Ahora es ↑ con una probabilidad del 100 %. Y sin embargo, no hemos actuado de ninguna manera sobre él.
Lo que repugnaba a Einstein
De alguna forma, lo que le ha sucedido al electrón 1 ha influido instantáneamente en el estado del electrón 2. Y esa misteriosa influencia se ha transmitido sin ningún soporte físico (ondas electromagnéticas o algo así). Además, las partículas podrían estar separadas millones de kilómetros y el efecto se produce exactamente igual. Parece una especie de telepatía entre los estados de los dos electrones. Y esto es lo que repugnaba profundamente a Einstein, ya que parece contradecir la teoría de la relatividad, según la cual ninguna influencia física puede transmitirse a mayor velocidad que la luz.
A pesar de su profundidad, el artículo de Einstein y compañía tuvo poco impacto en la comunidad científica. La mayor parte de los físicos consideró que estas disquisiciones eran discusiones bizantinas. A efectos prácticos, todo era semejante a una situación más convencional o “clásica”, en la que nosotros ignoráramos si los electrones tienen (los dos) el espín hacia arriba o hacia abajo. Y al medir el espín de uno de ellos, salimos de dudas respecto al espín del otro.
No habría ninguna transmisión de información. Solo habría ignorancia por nuestra parte del verdadero estado de espín de los electrones desde el comienzo.
Las desigualdades de Bell
Sin embargo, en 1964, el físico irlandés John Bell (el verdadero héroe de esta historia, y que sin embargo nunca recibió el Premio Nobel) probó que las cosas no son iguales al análogo clásico, en otras palabras, que el fenómeno del entrelazamiento podía demostrarse experimentalmente. La clave de la idea de Bell es utilizar muchos pares de partículas y permitir que los observadores de cada electrón (denominados Alice y Bob en la jerga científica) puedan medir el espín, no solo en la dirección vertical, sino también en otras direcciones.
Bell demostró que las medidas de Alice (digamos a₁, a₂, a₃, etc.) y Bob (b₁, b₂, b₃, etc.) se pueden combinar matemáticamente de una cierta manera, de forma que si la naturaleza es clásica (o sea, las magnitudes físicas están bien definidas y no hay transmisión instantánea de información), el valor de esa combinación ha de ser necesariamente menor o igual que 2.
Naturaleza clásica ⟹ f(a₁, a₂,… ; b₁, b₂,…) ≤ 2
Esto es lo que se llaman las desigualdades de Bell (hay otras formas equivalentes de expresarlas). Además, Bell demostró que en un estado cuántico entrelazado estas desigualdades se violan.
Física cuántica ⟹ f(a₁, a₂,… ; b₁, b₂,…) > 2
Así que ahora se iba a poder decidir experimentalmente entre las dos alternativas.
Los primeros experimentos
Aquí es donde entran en escena los investigadores galardonados, puesto que ellos fueron los pioneros en realizar experimentos que pusieron a prueba las desigualdades de Bell. Y el veredicto de la naturaleza ha sido claro: las desigualdades de Bell se violan, y además lo hacen en la proporción predicha por la física cuántica. Así que la teoría cuántica ha pasado airosa el test del experimento y, lo que es más importante, incluso si la física cuántica es reemplazada algún día por una teoría más perfecta, esta seguirá siendo no clásica, ya que las desigualdades de Bell se violan experimentalmente.
Estas contribuciones tienen un calado intelectual extraordinario, ya que nos muestran algo muy profundo y extraño sobre los mecanismos íntimos de la naturaleza. Además, han sido la base para el desarrollo de tecnologías con un potencial fabuloso, como la teleportación, la criptografía y la computación cuántica.
![]()
Alberto Casas González, Profesor de investigación, Instituto de Física Teórica (IFT - UAM - CSIC)
Este artículo fue publicado originalmente en The Conversation. Lea el original.
Comparte esto:
- Entrada
- Compartir en Threads (Se abre en una ventana nueva) Threads
- Compartir en WhatsApp (Se abre en una ventana nueva) WhatsApp
- Compartir en Reddit (Se abre en una ventana nueva) Reddit
- Compartir en Telegram (Se abre en una ventana nueva) Telegram
- Compartir en Mastodon (Se abre en una ventana nueva) Mastodon
- Compartir en Bluesky (Se abre en una ventana nueva) Bluesky